José Mata: Taxa marginal de substituição técnica

**Figura:** Taxa marginal de substituição técnica
$\begin{figure}\vskip.125in \par\beginpicture \centering\scriptsize\setcoordinate... ...inpicture \endpicture} at 0 0 \par\endpicture \par%%\vskip.15in \par\end{figure}$

À relação entre a poupança que a empresa pode realizar na quantidade empregue de um factor se aumentar a quantidade empregue de outro, de forma a manter a quantidade produzida constante, chamase a taxa marginal de substituição técnica. A taxa marginal de substituição técnica entre o capital e o trabalho $(TMST_{K,L})$ corresponde na Figura 1 à inclinação da recta que une os pontos

, que pode escreverse como

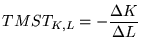$\displaystyle TMST_{K,L}=-{\Delta K \over \Delta L}$

(1)

Em geral esta taxa não é constante, embora existam casos de tecnologias específicas em que o é. A forma curva e convexa relativamente à origem que têm as isoquantas traduz o facto de que, em geral, a possibilidade de poupar capital com um determinado aumento do factor trabalho é tanto maior quanto menor for o nível de trabalho empregue ( $TMST_{K1,L1} > TMST_{K2,L2}$ no painel da esquerda da Figura 2).

**Figura:** Taxa marginal de substituição técnica ao longo de uma isoquanta
$\begin{figure}\vskip.125in \par\beginpicture \centering\scriptsize\setcoordinate... ... \par\put{\beginpicture \endpicture} at 0 0 \par\endpicture \par\par\end{figure}$

Se dividirmos quer o numerador quer o denominador da expressão anterior por $\Delta Q$ obtémse

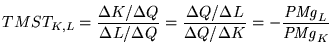$\displaystyle TMST_{K,L}={{\Delta K / \Delta Q} \over {\Delta L / \Delta Q}}={{... ...\Delta L} \over {\Delta Q / \Delta K}}= - {\mathit{PMg}_L \over \mathit{PMg}_K}$

(2)

tornandose evidente que a taxa marginal de substituição técnica também se pode expressar como um quociente entre as produtividades marginais do trabalho e do capital, um resultado que virá a ser útil um pouco mais adiante.

Outro aspecto importante é que muitas vezes estamos interessados em analisar o efeito de reduzir a quantidade de um factor em montantes muito pequenos. Quando isto acontece, ou seja quando $\Delta L$ tende para zero o quociente entre $\Delta K$ e $\Delta L$ é dado pela inclinação (o declive) da recta que é tangente à isoquanta em cada ponto. Quanto menos inclinada (mais horizontal) for esta recta, menor é o valor da taxa marginal de substituição técnica. O painel da direita da Figura 2 representa as tangentes à isoquanta nos pontos

, sendo a primeira destas tangentes claramente mais inclinada do que a segunda.

Até que ponto é que a empresa quererá aumentar a quantidade de trabalho e reduzir a de capital? A condição óptima passa por encontrar o ponto em que a recta de isocusto é tangente à isoquanta. Recordese que o declive da tangente às isoquantas em cada ponto representa a taxa marginal de substituição técnica que, como vimos atrás, reflecte o quociente entre as produtividades marginais dos factores. Por outro lado, o declive da recta de isocusto é dado pelo quociente entre os preços dos factores. A condição de optimalidade pode ser pois escrita como

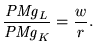$\displaystyle {\mathit{PMg}_L \over \mathit{PMg}_K} = {w \over r}.$

(3)

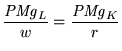$\displaystyle {\mathit{PMg}_L \over w } = {\mathit{PMg}_K \over r}$

(4)

que revela que o óptimo se atinge quando aquilo que se obtém por usar mais uma unidade adicional de um factor a dividir pelo custo que tem essa unidade adicional do factor for idêntico para todos os factores.