Incentivos: dedução algébrica

Escrevamos o lucro da empresa $\Pi$ como a diferença entre a produção

e o salário pago

$\displaystyle \Pi = Q - I$

(1)

A quantidade produzida é proporcional ao esforço dispendido

$\displaystyle Q = \alpha e$

(2)

O salário do trabalhador tem uma parte fixa e uma parte que varia com o esforço do trabalhador, podendo ser escrito como

$\displaystyle I = W + \beta e.$

(3)

O lucro pode pois ser escrito como

$\displaystyle \Pi = \alpha e - W - \beta e$

(4)

sendo o problema da empresa a escolha do nível de $\beta$ e de que lhe maximizam o lucro. O primeiro passo consiste na determinação no nível óptimo de esforço. Derivando $\Pi$ em ordem a e igualando a zero resulta

$\displaystyle \alpha = \beta.$

(5)

A utilidade do trabalhador varia positivamente com o salário que recebe e negativamente com o esforço que dispende . Admitamos que o esforço tem para o trabalhador um custo cada vez maior e que a utilidade pode ser escrita como

$\displaystyle U = I - \gamma e^2$

(6)

$\displaystyle I = U + \gamma e^2$

(7)

Para satisfazer a restrição de que o trabalhador quer aceitar o contrato proposto escolhemos o ponto em que a tangente a esta curva tem o mesmo declive da recta do salário.

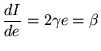$\displaystyle {dI \over de} = 2 \gamma e = \beta$

(8)

de onde resulta

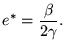$\displaystyle e^* = {\beta \over 2 \gamma}.$

(9)

Para um dado nível de utilidade mínimo o salário óptimo será

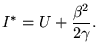$\displaystyle I^* = U + {\beta^2 \over 2 \gamma}.$

(10)

HTML check


Economia da Empresa > 8. Incentivos > Incentivos: dedução algébrica