José Mata Economia da Empresa
Economia da Empresa > 17. Oligopólio > O modelo de Stackelberg
 

O modelo de Stackelberg

Um modelo de concorrência em quantidades quando as empresas decidem sequencialmente.
A essência do comportamento estratégico está na antecipação que uma empresa pode fazer relativamente às rivais, criando assim uma situação de assimetria entre as empresas no mercado.

O primeiro modelo em que as empresas são assimétricas é um modelo devido ao economista alemão von Stackelberg. O modelo de Stackelberg é do tipo do de Cournot, em que as empresas decidem sobre as quantidades, com a diferença de que, em vez de decidirem simultaneamente, as empresas decidem uma após a outra. Existe uma empresa que é líder, que decide em primeiro lugar, e uma empresa seguidora que toma a sua decisão, tendo como um dado a decisão da primeira. Dito de outra forma, a empresa seguidora tomará a sua decisão de acordo com a sua função de reacção. A primeira empresa sabe que a segunda vai reagir desta forma e, ao tomar a sua decisão inicial leva em conta a previsível resposta da segunda. Uma vez tomadas, as decisões sobre as quantidades são irreversíveis. Tal como o modelo de Cournot, este modelo pode ser interpretado como envolvendo decisões iniciais sobre capacidades, seguidas de concorrência de preços à Bertrand.

Curvas de isolucro

Para determinar qual será o equilíbrio de Nash deste jogo convém voltar um pouco atrás à dedução das funções de reacção das empresas que fizemos a propósito do modelo de Cournot para introduzir um conceito novo, que vai ser útil para a análise deste modelo: as curvas de isolucro. Uma curva de isolucro representa das combinações das quantidades $ Q_1$ e $ Q_2$ que proporcionam a uma dada empresa um dado nível de lucro.

Na Figura 1 estão representadas três curvas de isolucro da empresa 1. As curvas de isolucro mais próximas do eixo horizontal do gráfico correspondem a níveis de lucro maiores para a empresa 1, sendo o nível máximo de lucro atingido quando a empresa 2 não produz nada e a empresa 1 produz a quantidade de monopólio $ Q_1^M$.

Figura 1: Curvas de isolucro
\begin{figure}\par\vskip.125in \par\beginpicture \scriptsize\setcoordinatesystem... ...r\put{\beginpicture \par\endpicture} at 0 0 \par\endpicture \par\par\end{figure}

Para um dado nível de produção da empresa 2, digamos $ Q_2'$, a empresa 1 pode atingir o nível de lucro $ \Pi_1^1$ se produzir a quantidade $ Q_1'$ ou a quantidade $ Q_1'''$. Quantidades intermédias entre $ Q_1'$ e $ Q_1'''$ permitem atingir curvas de isolucro mais perto do eixo horizontal e levam a níveis de lucro superiores.

De facto, se a produção da empresa 2 se mantiver inalterada, o aumento da produção da empresa 1 leva a um aumento da quantidade total do mercado, e a uma redução do preço. Numa primeira fase, enquanto a quantidade produzida pela empresa 1 é relativamente pequena, o efeito do aumento da quantidade mais do que compensa o efeito da redução do preço, e o lucro da empresa 1 aumenta. A partir de uma dada altura, o efeito da redução do preço passa a dominar e o aumento da quantidade produzida leva a uma redução do lucro da empresa 1.

Na Figura 1 este ponto ocorre quando a empresa 1 vende $ Q_1''$. Para esta quantidade produzida pela empresa 1, se a empresa 2 estiver a vender $ Q_2'$, o lucro da empresa 1 será igual a $ \Pi_1^2$. A empresa 1 não pode aumentar o seu lucro nem aumentando nem reduzindo a quantidade produzida. $ Q_1''$ é pois a quantidade óptima da empresa 1 se a empresa 2 estiver a produzir uma dada quantidade $ Q_2'$. Por conseguinte, o ponto ( $ Q_1'', Q_2'$) faz parte da função de reacção da empresa 1. Pelo mesmo raciocínio podemos concluir que a função de reacção da empresa 1 pode ser traçada unindo os pontos em que as diversas curvas de isolucro atingem a sua altura máxima.

Curvas de isolucro: dedução algébrica

A função lucro da empresa 1 deduzida a propósito do modelo de Cournot é do tipo

$\displaystyle \Pi_1 = (\alpha - \mathit{CMg} )Q_1 - \beta Q_1^2 - \beta Q_1Q_2.$ (1)

Fixando um dado nível de lucro ($ \Pi_1'$) e resolvendo para $ Q_2$ resulta

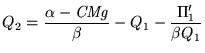$\displaystyle Q_2 = {\alpha - \mathit{CMg} \over \beta} - Q_1 - {\Pi_1' \over \beta Q_1}$ (2)

que é a função de isolucro da empresa 1 correspondente a $ \Pi_1'$.

Equilíbrio de Nash-Stackelberg

O equilíbrio no modelo de Stackelberg encontra-se da seguinte forma. A empresa seguidora vai decidir em cima da sua função de reacção ($ R_2$ na Figura 2). A empresa líder, por seu turno, sabendo isto, vai escolher a quantidade que lhe proporciona o maior nível de lucro possível, isto é, que lhe permite atingir uma curva de isolucro tão próxima do eixo horizontal quanto possível. Esta curva é a curva que é tangente à função de reacção da seguidora e o ponto de equilíbrio é dado pelo ponto $ S$. Relativamente ao modelo de Cournot, a empresa líder produz uma quantidade que é superior, ao passo que a seguidora produz uma quantidade inferior. Ou seja, o facto de decidir em primeiro lugar, permite à empresa líder ganhar uma vantagem relativamente à seguidora.

Figura: Equilíbrio de Nash-Stackelberg
\begin{figure}\par\vskip.125in \par\beginpicture \scriptsize\setcoordinatesystem... ...t 90 0 \par\put{\beginpicture \endpicture} at 0 0 \par\endpicture \end{figure}

No modelo de Stackelberg é crucial que uma vez tomada a decisão da empresa líder, esta não possa ser alterada. Se a empresa líder pudesse alterar a sua decisão, dada a decisão da empresa da empresa seguidora, a sua melhor decisão seria reduzir a produção de forma a ficar sobre a sua própria função de reacção. Nesse caso, contudo, a empresa seguidora não teria razão para tomar a decisão que tomou. Antecipando que a líder não fosse manter a quantidade inicial, e efectuando o raciocínio sofisticado subjacente ao modelo de Cournot, a seguidora produziria a quantidade correspondente ao equilíbrio de Cournot.

Equilíbrio de Stackelberg: dedução algébrica

Consideremos as funções procura e custos habituais.

A empresa seguidora ($ S$) toma a sua decisão de acordo com a sua função de reacção, dada a quantidade produzida pela empresa líder ($ L$).

$\displaystyle Q_S = {\alpha - \mathit{CMg} \over 2\beta } - { 1\over 2}Q_L.$ (3)

A empresa líder vai tomar a sua decisão maximizando o seu lucro dada a reacção da empresa seguidora

$\displaystyle \Pi_L = Q_L (P-\mathit{CMg} )=Q_L(\alpha - \mathit{CMg} - \beta (Q_L+Q_S))$ (4)

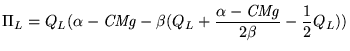$\displaystyle \Pi_L = Q_L(\alpha - \mathit{CMg} - \beta (Q_L+{\alpha - \mathit{CMg} \over 2\beta } - { 1\over 2}Q_L))$ (5)

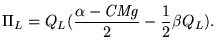$\displaystyle \Pi_L = Q_L ({\alpha - \mathit{CMg} \over 2} - { 1\over 2}\beta Q_L).$ (6)

A maximização do lucro da empresa líder implica

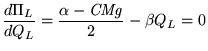$\displaystyle {d\Pi_L \over d Q_L} = {\alpha - \mathit{CMg} \over 2} - \beta Q_L=0$ (7)

de onde resulta

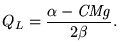$\displaystyle Q_L = {\alpha - \mathit{CMg} \over 2\beta}.$ (8)

Substituindo em 3 obtém-se a quantidade produzida pela empresa seguidora

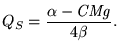$\displaystyle Q_S = {\alpha - \mathit{CMg} \over 4\beta}.$ (9)

Quem é o líder?

O modelo de Cournot é um ponto de referência natural para a análise do modelo de Stackelberg, podendo o equilíbrio de Stackelberg ser visto como o resultado de uma estratégia de antecipação da empresa líder. O modelo não nos diz onde é que está a origem da assimetria existente entre as empresas e por que é que uma é líder e a outra seguidora.

Um contexto onde existe uma razão natural para esta assimetria é o contexto em que existe uma empresa instalada no mercado e outra que vai entrar nesse mesmo mercado. Nesse contexto, é natural que a empresa instalada tenha a iniciativa e decida sobre a capacidade a instalar. Parece também razoável que, se o investimento em capacidade for irreversível, a entrante decida assumindo a capacidade instalada como um dado. Neste modelo, se os custos fixos forem tais que a quantidade $ Q_S$ correspondente ao equilíbrio seja inferior à dimensão mínima necessária para operar com rentabilidade, então a vantagem de se ter movido em primeiro lugar permite à empresa líder impedir a entrada da seguidora. Admitindo que a entrada ocorre, o equilíbrio será dado pelo ponto $ S$, e a empresa instalada obtém um lucro correspondente a $ \Pi_1^*$. Se a entrada não ocorrer, o equilíbrio será dado pelo ponto $ M$, ponto esse a que corresponde um lucro claramente superior para a empresa líder.
© 2000 José Mata
Design: Arte Numérica

HTML check