Equilíbrio de Stackelberg: dedução algébrica

Consideremos as funções procura e custos habituais.

A empresa seguidora () toma a sua decisão de acordo com a sua função de reacção, dada a quantidade produzida pela empresa líder ().

$\displaystyle Q_S = {\alpha - \mathit{CMg} \over 2\beta } - { 1\over 2}Q_L.$

(1)

A empresa líder vai tomar a sua decisão maximizando o seu lucro dada a reacção da empresa seguidora

$\displaystyle \Pi_L = Q_L (P-\mathit{CMg} )=Q_L(\alpha - \mathit{CMg} - \beta (Q_L+Q_S))$

(2)

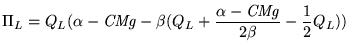$\displaystyle \Pi_L = Q_L(\alpha - \mathit{CMg} - \beta (Q_L+{\alpha - \mathit{CMg} \over 2\beta } - { 1\over 2}Q_L))$

(3)

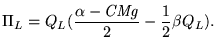$\displaystyle \Pi_L = Q_L ({\alpha - \mathit{CMg} \over 2} - { 1\over 2}\beta Q_L).$

(4)

A maximização do lucro da empresa líder implica

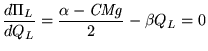$\displaystyle {d\Pi_L \over d Q_L} = {\alpha - \mathit{CMg} \over 2} - \beta Q_L=0$

(5)

de onde resulta

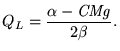$\displaystyle Q_L = {\alpha - \mathit{CMg} \over 2\beta}.$

(6)

Substituindo em (1) obtém-se a quantidade produzida pela empresa seguidora

$\displaystyle Q_S = {\alpha - \mathit{CMg} \over 4\beta}.$

(7)


Economia da Empresa > 17. Oligopólio > Equilíbrio de Stackelberg: dedução algébrica